今回は「三角関数っていつから習うの?」「どんな公式があるの?」といった疑問にお答えします。
三角関数は、高校数学で必ず学ぶ重要な単元。
ちょっと難しそう…と思うかもしれませんが、公式や計算方法を一つ一つ理解すれば、必ずマスターできますよ!
この記事では、初心者でも分かるように授業風に解説していきますので、一緒に学びましょう!
三角関数いつ習う?高校での学習時期と基礎を解説

三角関数を学ぶタイミングは、主に高校2年生の数学Ⅱで登場します。
高校数学の中でも、三角関数は図形や関数の計算で多く使うので、「この先ずっと役立つ知識」として学んでいきます。
三角関数を学ぶタイミングは高校2年生が基本
高校で学ぶ三角関数は、三角比の延長線上にあります。中学で「三角比」を習ったことを覚えていますか?
たとえば、直角三角形の辺の比率で、

という公式を学びましたね。
この三角比を、より広い範囲で活用できるようにしたのが「三角関数」です。
高校2年生で学ぶ理由は、この段階で「関数」や「座標平面」の知識が土台として身についているからです。
文系と理系で三角関数の扱いに違いはある?
文系と理系では、数学のカリキュラムに違いがあります。
文系では基礎的な三角関数だけを学びますが、理系ではより高度な内容に進みます。例えば以下のような内容です。
- 文系:三角関数の基本公式と簡単なグラフ
- 理系:三角関数の微分や積分、合成公式の応用
理系を目指す場合は、三角関数をしっかり理解しておくことが非常に重要です。
三角関数を学ぶ理由とは?数学Ⅱの重要単元
三角関数を学ぶ理由は、大きく分けて2つあります。
- 日常生活や科学技術で活用される
測量や建築で使われるのはもちろん、音波や光波、電波の分析にも三角関数が使われています。 - 他の単元と深く関わる
例えば、ベクトルや微積分の計算でも三角関数を使うことがあります。高校数学の中でも「基礎中の基礎」と言える単元です。
中学で学ぶ三角比と三角関数の関係
中学で学んだ三角比と三角関数は、計算の仕組みこそ同じですが、定義が少し異なります。
中学では「直角三角形」の中だけで扱っていた三角比ですが、高校では「単位円」を使い、すべての角度に対応できるようにします。
たとえば、角度が 90°を超えたときも、以下のように三角関数を計算できます。
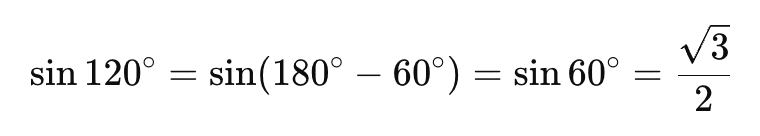
単位円を使うと、どんな角度にも対応できるのが三角関数の魅力です!
高校入試で必要?三角関数が登場する場面
高校入試では、三角関数そのものは出題されません。ただし、中学で学ぶ三角比を使った問題がよく出題されます。
以下は典型的な例です。
例題: 高さ10mの塔があり、地上から見上げた角度が30° でした。このとき、塔から地上の観測点までの距離を求めなさい。

このように、三角比の計算を確実にしておくと、三角関数の理解もスムーズになります。
三角関数いつ習うか分かった後に:公式や合成を分かりやすく

三角関数の公式は、計算問題で頻出する重要事項です。
ここでは、基本公式から合成公式まで分かりやすく解説します。
角関数の基本公式一覧【覚え方と使い方】
三角関数の基本公式をまとめます。以下の公式は必ず覚えておきましょう!
1.加法定理

2.倍角の公式
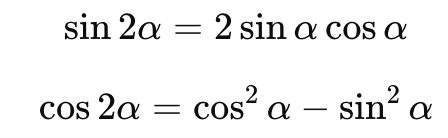
3.三角関数の相互関係
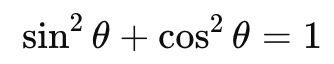
これらの公式は、三角関数の計算に不可欠です。
三角関数の合成とは?公式と具体例を解説
三角関数の合成とは、以下のように複数の三角関数を1つにまとめることです。
合成公式(sinの場合)

ただし、 αは以下の関係を満たします。
具体例:

ここで、αを求めると、
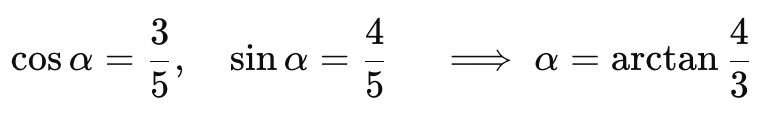
加法定理とその応用例【公式の背景を理解】
加法定理は三角関数の基礎中の基礎で、合成公式や微分・積分の計算にも欠かせません。公式は次の通りです。
加法定理

これらは、単位円上の座標を考えることで導き出すことができます。
具体例: 例えば、sin(45°+30°)を計算してみましょう。

値を代入すると、
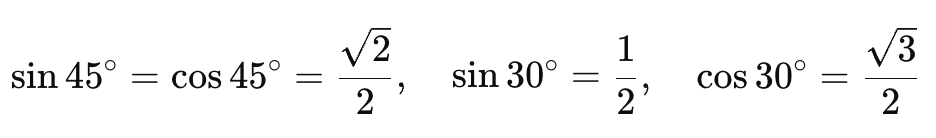
計算式は次のようになります。

このように、加法定理は異なる角度を持つ三角関数の計算に役立ちます!
三角関数の微分・積分の基礎と応用範囲
三角関数の微分と積分は、数学Ⅲや物理で重要な役割を果たします。まずは公式を確認しましょう。
微分公式

積分公式

以下の式を計算してみましょう。
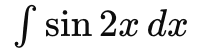
ステップ1:積分公式を利用します。

ステップ2:積分定数 C を追加することを忘れないようにします。
微分と積分は、グラフや面積の計算にも応用できるため、基礎をしっかり押さえておきましょう!
三角関数を学ぶ上でつまずきやすいポイントと克服方法
三角関数は多くの生徒が苦手意識を持ちやすい単元ですが、ポイントを押さえれば理解が進みます。
- つまずきやすいポイント:
- 単位円と角度の関係を理解できない
- 合成公式や加法定理を暗記で終わらせてしまう
- 公式を使う場面がイメージできない
- 克服方法:
- 単位円の図を活用する:角度がどの象限にあるかを視覚的に把握しましょう。
- 公式の導出を繰り返す:公式を暗記ではなく、自分で導けるように練習することで応用力がつきます。
- 具体的な例題を解く:問題に触れることで、公式の使い方を身に付けましょう。
総括:三角関数いつ習う?のまとめ
最後に、本記事のまとめを残しておきます。
三角関数を学ぶタイミング
- 三角関数は高校2年生の数学Ⅱで学ぶ。
- 三角比の延長として学び、単位円を使うことですべての角度に対応する。
文系と理系での扱いの違い
- 文系:基本的な三角関数の公式や簡単なグラフを学ぶ。
- 理系:微分・積分、合成公式の応用など高度な内容を学ぶ。
三角関数を学ぶ理由
- 日常生活や科学技術(測量、建築、音波解析など)で活用される。
- 他の単元(ベクトル、微積分)との関連が強い重要単元。
中学で学ぶ三角比との違い
- 中学:直角三角形内の計算に限定される。
- 高校:単位円を使い、すべての角度(90°以上や負の角度)に対応できる。
高校入試との関係
- 三角関数そのものは出題されないが、中学で学ぶ三角比が頻出。
三角関数の基本公式
- 加法定理、倍角の公式、三角関数の相互関係が中心。
- 計算に不可欠であり、しっかりと暗記する必要がある。
三角関数の合成
- 複数の三角関数を1つにまとめる方法(合成公式)が重要。
加法定理の応用
- 異なる角度を持つ三角関数の計算に活用される。
- 単位円を用いた視覚的な理解がポイント。
微分・積分の基礎と応用
- 微分と積分の公式を覚えることで、物理や数学Ⅲでの応用が可能。
- グラフや面積の計算にも役立つ。
つまずきやすいポイントと克服方法
- 単位円と角度の関係、公式の暗記だけに頼らない。
- 公式の導出を繰り返し、具体例を通じて理解を深める。
総括
- 三角関数は高校数学の基礎であり、多くの場面で役立つ。
- 基礎を固め、応用力をつけることが重要。
