約分のやり方の裏ワザを紹介！簡単なしかた&早くする方法を解説

こんにちは！塾長です。

今日は「分数の約分」について、楽しく簡単に学べる「裏ワザ」をたっぷり紹介します！

「分数の計算が苦手…」「約分って時間がかかる…」そんな悩みを解消できるように、わかりやすく解説していきますよ。

途中式も丁寧に見せながら進めますので、苦手な子でも安心してくださいね！

この記事を読んで、ぜひ算数をもっと好きになりましょう！

約分の裏ワザ：初心者でも簡単に分かる効率的なやり方

約分は分数の分母と分子を小さな数字にして、見た目をスッキリさせるために行います。でも、普通の方法だと時間がかかることも。

そこで「裏ワザ」を使えば、もっと簡単に素早く約分できるようになります！

ではさっそく、いくつかの方法を見ていきましょう。

約分の基本をおさらい：なぜ約分が必要なのか？

まずは基本から確認していきましょう。

分数の「約分」とは、分母と分子を同じ数字で割り算して、もっとシンプルな形にすることです。

たとえば、次のような計算を考えてみてください。

この分数を約分すると、次のようになります。

1. 分母と分子の共通の約数「2」を見つけます。
2. 分母と分子をそれぞれ2で割ります。

結果、元の分数は 3/4​ に簡単化されました！見た目がスッキリするだけでなく、計算も楽になりますよね。

「分母と分子の差」を使った約分の裏ワザ

さて、ここからが「裏ワザ」の登場です！

分母と分子の「差」に注目することで、効率よく約分することができます。具体例で見てみましょう。

この分数を約分するには、まず 分母と分子の差 を計算します。

次に、この差「46」の約数を確認します。「46」の約数は「1, 2, 23, 46」です。この中で分母と分子を割り切れる数字を探しましょう。

試してみると、「23」で割れることがわかります。

なんと、簡単に約分できました！この方法を覚えれば、大きな数字でもスムーズに約分できます。

素因数分解を使った約分の効率化

次に、素因数分解を使った方法を見てみましょう。

たとえば、次の分数を約分するとします。

まず、分母と分子を素因数分解します。

• 42 = 2×3×7
• 56 = 2×2×2×7

次に、共通している素因数を取り除きます。この場合、共通の素因数は「2」と「7」です。

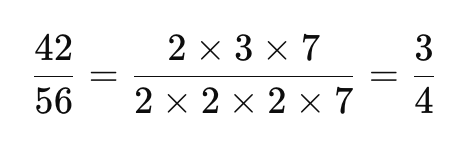
この方法は少し手間がかかりますが、確実に正しい結果が得られます！

倍数判定でスピードアップ！約分に使える数字を見つけるテクニック

「倍数判定」は計算を速くする鍵です。以下のルールを覚えておくと、すぐに割り切れる数字がわかります。

1. 2の倍数 → 偶数（末尾が「0, 2, 4, 6, 8」）
2. 3の倍数 → 各桁の合計が3の倍数
3. 5の倍数 → 末尾が「0」または「5」

例として、次の分数を考えます。

分母と分子は偶数なので、まず2で割ります。

次に、3の倍数かどうかを判定します。分子「27」の各桁を足すと 2+7=9、分母「36」も 3+6=9 で、どちらも3の倍数です。

さらに3で割ると…

これで完成です！倍数判定を使うと、一気に約分できますね。

1桁の公約数から始めよう

最後に、初心者におすすめの方法を紹介します。

それは「1桁の公約数から試す」ことです。たとえば、次の分数を見てみましょう。

まず、1桁の数字「2, 3, 5, 7」などで割れるか試します。

• 36と48は両方2で割れます。

次にもう一度、同じ数字で割れるか確認します。

最後に、さらに割れる数字がないかチェックします。

「3」で割れるので…

この方法なら、確実にシンプルな形にできます！

約分のやり方の裏ワザ：効率的な約分を可能に

約分の裏ワザを習得したら、次のステップは実践練習です。この章では、初心者から上級者まで使える練習法や、試験や日常生活での応用例を紹介します。

間違いやすいポイントや他の数学分野への発展も併せて解説するので、スキルを着実に高めていきましょう！

練習問題で約分の裏ワザをマスター

約分のスキルを磨くには、実際に問題を解くことが最も効果的です。以下の問題集を使って裏ワザを試してみましょう。

初心者向け練習問題：

1. 12/18
   • 裏ワザ：両方とも 6 の段にあるため、直接 6 で割る。
   • 答え：2/3
2. 16/24
   • 裏ワザ：分子と分母の差 24−16=8。8の約数（1, 2, 4, 8）から 8 で割れる。
   • 答え：2/3

中級者向け練習問題：

1. 35/50​
   • 裏ワザ：一の位の法則を使い、5 で割る。
   • 答え：7/10
2. 48/72
   • 裏ワザ：九九を使って 6 の段で割る。
   • 答え：2/3

上級者向け練習問題：

1. 144/216
   • 裏ワザ：素因数分解で共通因数を見つける。
   • 答え：2/3
2. 275/825
   • 裏ワザ：差 825−275=550 を使い、共通因数 25 で割る。
   • 答え：1/3

時間短縮の鍵：試験で役立つ約分テクニックの応用例

試験では時間が限られています。ここで紹介するテクニックを使えば、時間を節約しながら正確な解答を導けます。

応用例1：一の位をチェックする

• 例題：90/150
  • 一の位が 0 と 0 なので 10 で割る。
  • 90/150=9/15 → 3 で割り、答えは 3/5。

応用例2：素数で割る判断力

• 例題：161/115
  • 差 46 の約数を利用し、23 で割る。
  • 答え：7/5

裏ワザが役立つ場面とは？約分で解ける日常生活の問題

約分は日常生活でも役立ちます。以下の例を見てみましょう。

1. レシピの分量調整

• 問題：4人分のレシピを3人分に調整。材料が 12/4​ 杯の場合。
• 解決：12/4=3。簡単に調整できます！

2. 割り勘計算

• 問題：2750円を11人で割る。
• 解決：2750/11 を約分すると 250。1人250円です。

間違いやすい約分の罠：よくあるミスとその回避方法

ミス1：途中で約分を終わらせる

• 例：20/30を 2/3​ まで約分せず、10/15​ で終わる。
• 対策：必ず「さらに割れるか確認」する習慣を。

ミス2：大きい数でいきなり割ろうとする

• 例：144/216 を最大公約数 72 で割ろうとして混乱する。
• 対策：小さな数から順番に割る。

さらに計算が楽になるコツ：他の数学分野への応用方法

約分は他の数学分野でも活用可能です。以下のような場面で役立ちます。

1. 通分での応用

• 例題：3/4+5/6​
  • 通分後、分母が 12 になり、分子は 9+10=19。
  • 答え：19/12。

2. 分数の乗除計算

• 例題：18/24×16/20
  • 約分を先に行い、3/4×4/5=3/5。

総括：約分のやり方の裏ワザまとめ

最後に、本記事のまとめを残しておきます。

約分の基本:

• 分母と分子を同じ数字で割り、分数を簡単な形にする作業。
• 見た目がスッキリし、計算が楽になる。

裏ワザ1: 分母と分子の差を使う方法:

• 差の約数を確認し、それを使って分数を約分。
• 例: 161/115 → 差 46 → 約数 23 で割る。

裏ワザ2: 素因数分解:

• 分母・分子を素因数分解し、共通因数を見つけて取り除く。
• 例: 42/56​ → 素因数分解で約分。

裏ワザ3: 倍数判定の活用:

• 特定の数字（2, 3, 5など）で割り切れるかを簡単に判定する方法。
• 例: 54/72 → 2で割る → 次に3で割る。

練習問題でスキルアップ:

• 初心者向けから上級者向けまでの例題を使い、効率よく約分を練習。
• 具体例とともに解法を解説。

試験での応用:

• 一の位や素因数を活用して計算スピードを向上。
• 試験での時間短縮に役立つ。

日常生活での活用:

• レシピの分量調整や割り勘計算で約分を使い、効率化。
• 例: 4人分から3人分のレシピ調整など。

間違いやすいミスと回避法:

• 途中で約分を終わらせるミスや大きい数で割ろうとするミスを防ぐためのアドバイス。
• 小さな数から順に割るのがポイント。

他分野への応用:

• 通分や分数の乗除計算での応用方法を紹介。
• 例: 3/4+5/6 の通分計算。

結論:

• 約分の裏ワザを学ぶことで、算数・数学が楽しく効率的になる。
• 練習と実践を繰り返すことで、さらなるスキルアップが可能。