兵庫県の公立高校入試の数学はどのように対策をすればいいのでしょうか?
本記事では、実際に兵庫県公立高校入試専門の塾を運営している塾長自らが、現場でも取り入れている対策を完全無料で公開します。
数学においては大問ごとに攻略法が異なると思っているので、大問別に対策を分けて紹介し、その際は塾の中でも使用しているテキストを合わせて紹介します。
なお、紹介するテキストは原則として塾専用教材であり非売品です。そのため市販の書店などでは購入出来ず、学習塾を通してしか購入できません。しかし、Amazon(※楽天は不可)であれば、一部個人販売がなされています。もし購入する際は、Amazonであれば購入可能です。
兵庫県公立高校入試:数学の対策(大問別問題集ルート)
兵庫県の公立入試の数学では、大問ごとに対策を変えるのが合理的です。満点が狙える大問や、対策しやすい大問、対策しずらい大問があるからです。
そのため、ガムシャラに勉強するのは非常に効率が悪く、「取れるところをきちんと対策して取る」「取れる期待値が低いところは対策はほどほどに」のマインドが実は大事です。
大問1:小問集合の対策&使用教材
まず、兵庫県では長年にわたり大問1は「小問集合」です。参考までに令和7年度の大問1を載せておくと、以下の通りです。

問題数は全部で8問で配点は全て3点です。つまり、大問1だけで24点分出題されることになります。
そして、大問1は難易度が非常に低く、数学がどれだけ苦手な人でも、確実に満点を狙っていかなければならない問題です。後述しますが、これ以降の大問は一定の地頭を有していないと、平気で大問丸ごと落とすことがあり得ます。
そういう意味では、塾などの対策でも唯一再現性高く努力させれば満点に近づけさせることができるブロックということになります。
対策の方法ですが、まずは夏休みには「大問1の完成」という塾専用教材を全体の2/3ほど進めます。(残り1/3は中3範囲も含んでしまうので、夏休みだとそこまでしかできない。)

「大問1の完成」は全国の都道府県の小問集合のみを集めたシャッフル問題集です。見開き1ページがセットになっていて、正の数・負の数の計算、方程式、図形問題、確率問題などあらゆるジャンルの問題を1ページにシャッフル形式で載せています。
こんな感じ↓

自塾の場合、夏期講習の数学の最初の授業で大問1の完成を時間を測ってテストします。夏休みは毎授業の最初に必ずやるようにしていますが、全ては受験の大問1で満点を取らせるためです。
なお、この手のシャッフル問題集で全然点が取れない生徒は、受験問題集をやる前にもっと基礎的な計算問題集で反復練習をしてください。学校のワークや、通年ごとに塾で渡される学年別問題集のA問題レベルの問題を全部こすればOKです。
また、大問1の完成の2/3をやり切ったら、次は「計算の達人」というこれまた小問集合を寄せ集めた問題集を使って追加演習をしていきます。

こちらは、1ページが1セットで毎回5題シャッフル問題が演習できます。回数を重ねるごとに難易度が上がり、出題範囲も3年生の割合が増えてきます。前半は中3範囲をほぼ含まないので、中3の夏休みから使えます。
中身はこんな感じです。

この問題集は、大問1の完成が終わり次第取り組ませています。基本的には夏休みの終盤から使います。もちろん夏休みだけでは終わらせる必要はなく、受験問題の場合は9月以降の通常授業の最初の10分で毎回演習時間をとってやらせます。
この手の問題集は一気にやるのではなく、5〜10問ぐらいを3日に1下位ペースぐらいでやらせて、記憶から抜けさせないようにしてほしいと思います。受験までコツコツやらせて1周回すとかでも全然OKです。もちろん、早めに1周して何回も反復する的な使い方も効果的です。
なお、塾用教材は購入してから届くまでに少し時間がかかるので、なるべく早めに注文しておくことをおすすめします。数にも限りがあるので、なくなり次第買えなくなるリスクも大きく、魅力的に感じる人は今すぐポチらないと後から買えなくなるかもしれません。
関数分野の大問対策:使用教材や目標ライン
小問集合の次に優先して対策をして欲しいのが、「関数分野」です。
関数分野は、中2で習う「1次関数」、中3で習う「2次関数」の2つがありますが、いずれも入試頻出論点です。必ず重点学習で関数をやり込むフェイズが受験生には必要になります。
なお、兵庫県の場合は例年は1次関数(と方程式を混ぜた問題)で大問1つ、2次関数と図形を絡めた問題で大問を1つ作ることが多いです。
1次関数はこんな感じの問題↓が多いです。
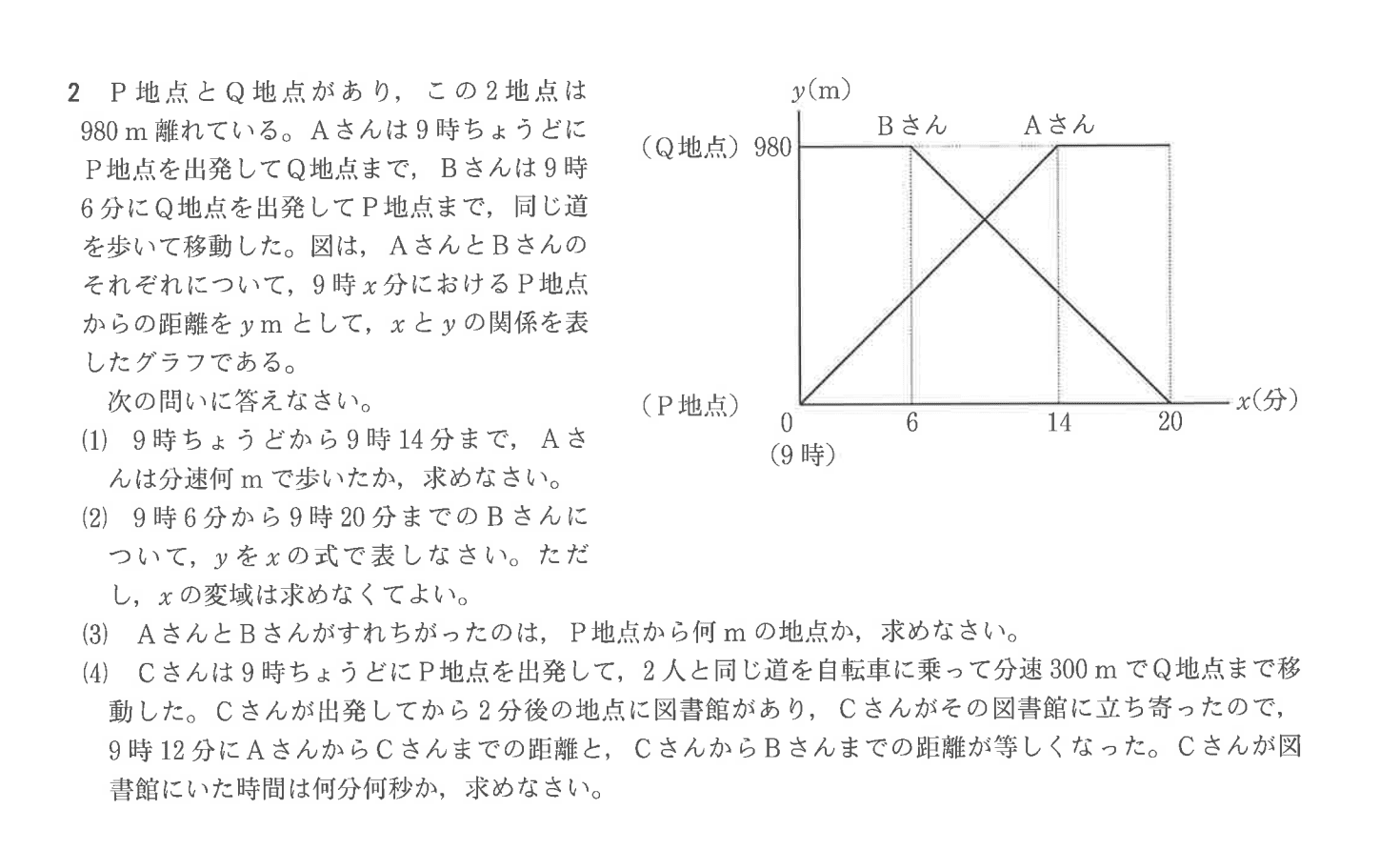
2次関数は、だいたいこんな感じ↓です。
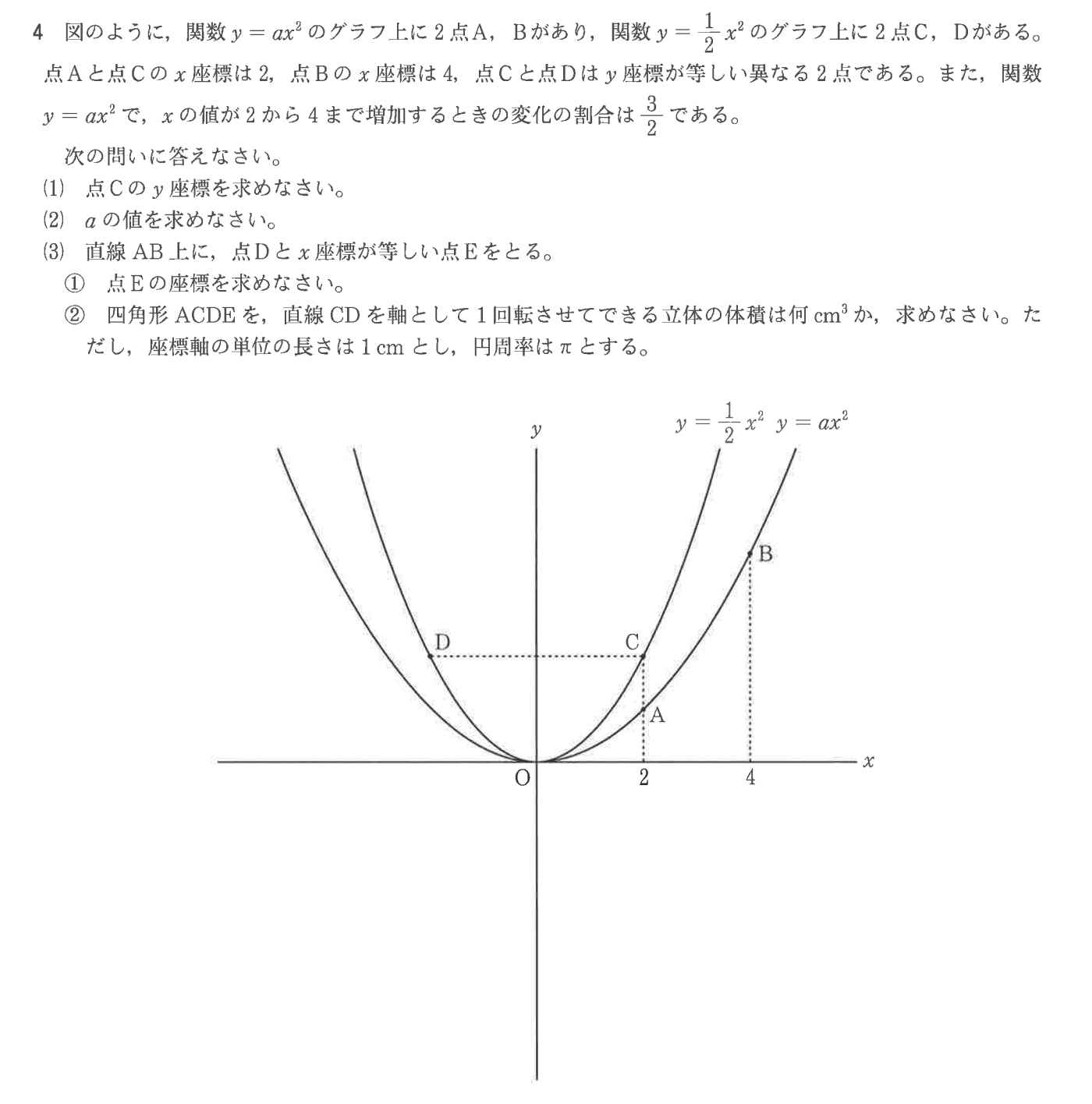
なお、最近の変更点としては、今までは確実に1次関数系の文章題が1つ出題されていましたが、令和7年度で初めてその流れが打ち切られ、方程式と式の証明を絡めた問題が出されました。
こんなの↓です。

しかし、こうなると対策は非常に複雑になります。
なぜなら、こっち系の問題ってある程度長い文章で設定条件を決められ、読解した上で数的な処理を求められるからです。もちろん、受験対策で見たことがあるような問題ではなく、ほぼ間違えなく初見で見るような問題になります。
だから、一定の読解力があり、その上で数学的に何をすればいいのかを把握する能力が求められてしまい、覚えていたことをそのまま実践するだけみたいな猿真似は通用しません。
ハッキリ言いますが、地頭(読解力や数的センス)が乏しい生徒に再現性高くこれらの大問で得点させることは塾でも難しいです。IQが低い子だと問題文の意味がわからず、設定条件を理解する段階で詰みます。当然ですが、大問丸々落としてしまい、この時点で15点全て失点ということは決して珍しくありません。
そういう意味では、1次関数の文章題や方程式に関する大問は人を選びます。だから、対策していたからと言って決して再現性高く点数が安定するとは思わない方がいいです。一定ラインできる子でも年によってはハマらず大きく失点するリスクが高いのがこの手の大問の特徴です。
でも、2次関数と図形を絡めた大問は、まあまあ再現性高く点数を取りにいけます。理由は王道の問題集に収録されているようなパターン問題が多く出題され、初見殺しに合うリスクが比較的低いからです。
自塾の場合は、関数に特化した問題集「関数の達人」を使用し、この2次関数に特化した大問を攻略するための対策を行います。

関数の達人は、比例・反比例、一次関数、二次関数の文章題および図形融合問題に特化した問題集です。だから、この1冊で兵庫受験の大問最大2つ分の対策を1冊で行える神問題集です。
導入で基礎基本技を演習する部分があり、その後は「実践演習」という問題ページで各都道府県で出題された関数の良問を大量に収録しています。
導入レベルの基礎問↓

実戦演習↓
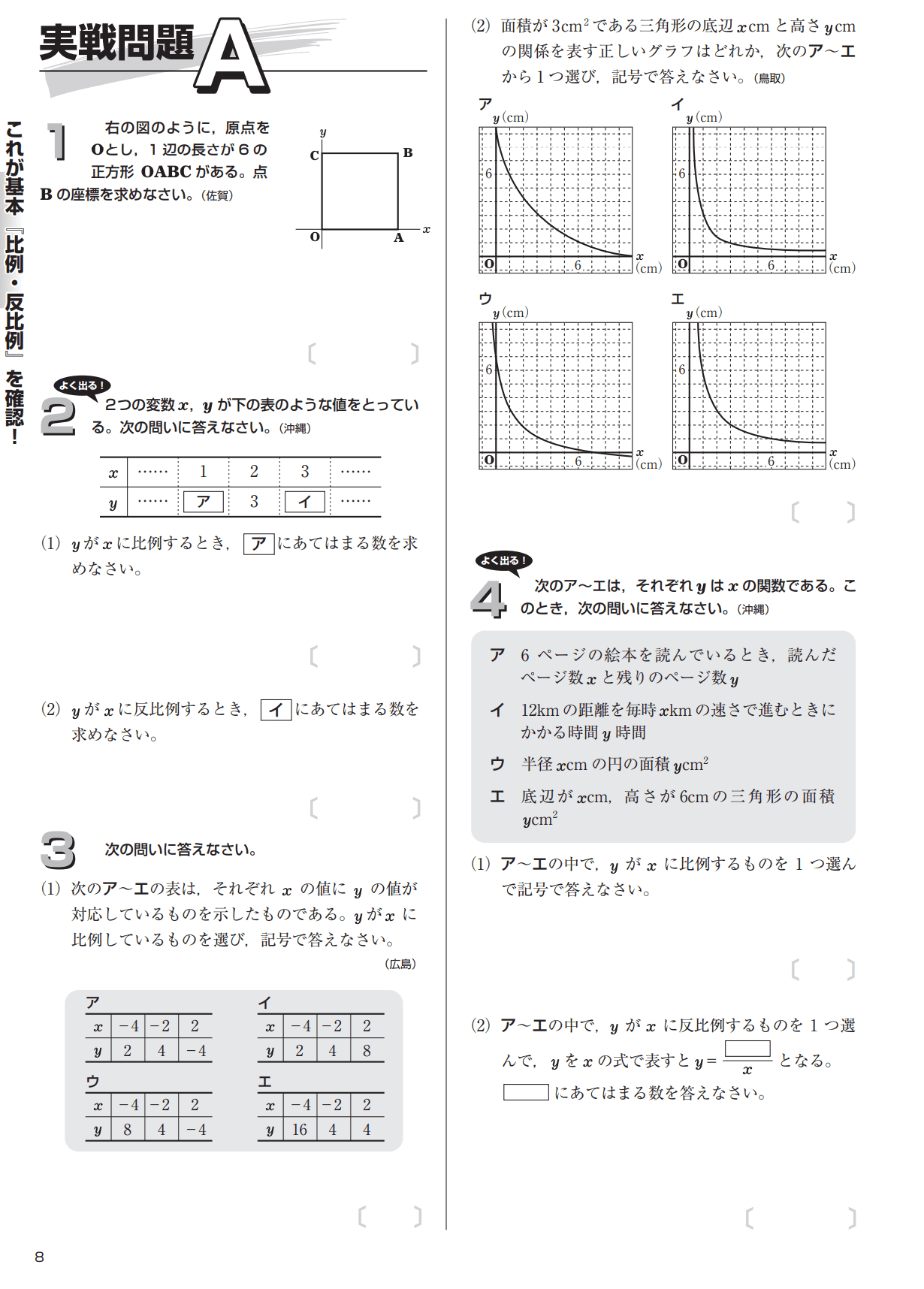
基本的な戦術としては、中3の夏休みに関数の達人を使って授業をして、まずは基礎定着をさせます。そして、塾の中で演習時間をとって「実践問題A」までをやらせます。その上で夏休みの最終週に実戦問題Aのみを再試して全問正解できるレベルを目指させます。
正直夏休みにここまで仕上げられると、その後の対策がグッと楽になります。この後9月以降からは兵庫模試などの過去問で演習させますが、関数の達人で練習した技がかなり生きてきます。
関数の達人は夏休みから始めて、受験直前まで何度でもこすれる関数のバイブル本です。これも絶対に購入して使って欲しい超おすすめ問題集の1つです。
ちなみに、関数の達人のような受験問題集がまだ早い生徒(偏差値60以下)は、通常の塾用教材を使って、定期テスト対策レベルの問題からやることをおすすめします。
まず1次関数対策ですが、1次関数は中2範囲なので、中2の数学問題集を1冊やりましょう。おすすめは自塾でも使用しているテキストの1つ「ステップ式数学 中2」です。

後述しますが、兵庫の大問の1つ図形分野の対策(合同の証明など)でも使えるので、コスパの良い問題集です。
また、中3の二次関数分野は中3範囲なので、中3用の基礎問題集もおすすめです。教材は同じく「ステップ式数学 中3」です。

こちらは中3通年用教材ですので、同じく図形分野の対策として相似・円周角・三平方などの対策でも併用できるのでコスパもいいです。夏休みに2次関数の予習をする際にも重宝します。
ステップ式は通年用の問題集ですが、収録されている練習問題は受験対策としても非常に効果的なので、もはや受験対策用の問題集と言ってもいいのでは?と毎年思えるような神教材です。
確率やデータに関する大問攻略:使用教材など
ここまでは、小問集合の大問1つ、関数及び方程式の大問2つを攻略する手順を紹介してきましたが、次は「確率・データ」です。
兵庫の場合、確率の問題かデータ問題で毎年1つ大問が作られます。比率で言えば圧倒的に「確率」の方が多く、データ問題が出る年はレアです。そのため、普段の勉強の比重としては確率を重点対策させることになります。
なお、確率の問題はこんな感じです。

問題の傾向としては、純粋に確率の定番問題だけを出すというより、他分野の知識を融合させて問題を作ってくる感じです。上記の問題も整数問題との融合です。
だからまあ、確率も同様に再現性高く高得点を取らせることが難しい分野だと思ってください。あと、年によってイージーな年と激ムズの年があり、問題ガチャの要素も非常に大きいです。
ただし、1次関数の文章題や方程式よりは地頭要因の影響が少なく、対策によって点数を取らせやすいとも言えます。そういう意味では、対策時間を文章題系の大問より増やすのも1つの戦略です。ここはその子次第なので、塾でコンサルしてあげないといけません。
なお、確率は中2範囲なので、大問対策としては中2用の問題集を基本的に使えばOKです。関数のところで紹介した「ステップ式数学 中2」をメインテキストにすればOKです。
ただし確率は問題演習の量を増やして欲しいので、もう少し問題集を追加します。例えば「WinPass 数学中2」のような同レベルの難易度の問題集をもう1冊回すのは効果的です。
中2用の問題集は1次関数もあるし、図形問題も豊富なので複数買っても損はしません。演習量を担保できそうなら数学に関しては問題集を増やしてもいいと思います。
ただ、学年別問題集は受験レベルから見ると少し優しいです。
よって、ある程度基礎がために自信が持てるようになると、「データ問題・確率の達人」という大問特化受験問題集をやるのがおすすめです。

この問題集は確率とデータに特化しており、まさに兵庫県の大問のために用意されたような問題集です。レベル的には最終ゴールに据える問題集で、過去問演習に入る前に1冊回して自信をつけるために使用して欲しいです。
入試過去問の良問を厳選しているのでかなり力がつきます。
こんな問題↓

タイミング的には夏休みに始められる子はスタートしても全然OKです。基礎固めが怪しい子は、夏休みは標準レベルの問題集に振り切り、12月ぐらいから徐々にやり始めるとかでも全然間に合います。決して分厚い問題集ではないので、やり始めれば意外とスッと行きます。
図形の大問攻略:証明だけガチれ
兵庫県では、図形分野に特化した大問が必ず1題は出題されます。
こんな感じです。
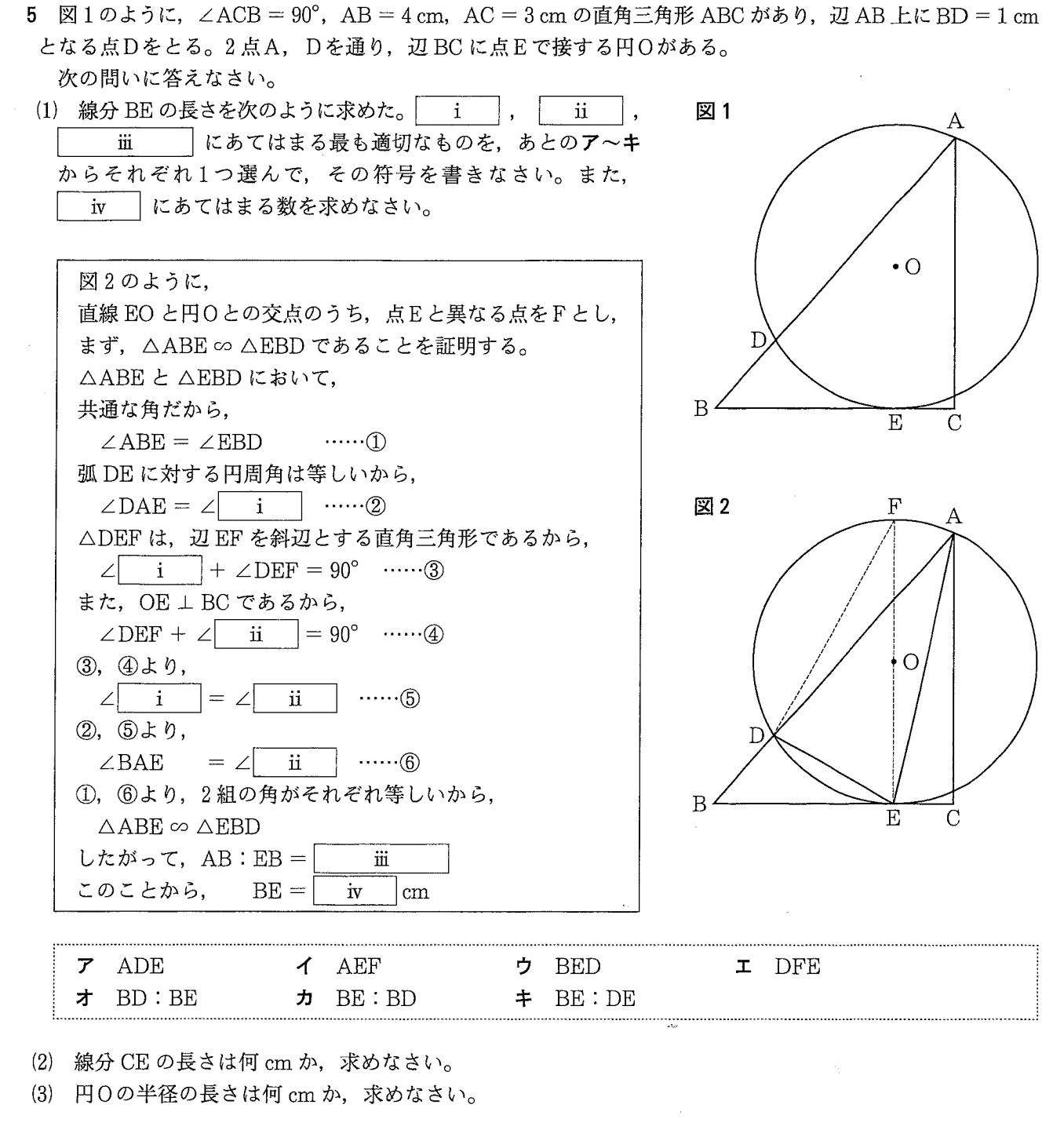
基本的には(1)で証明問題の穴埋めが出題されます。兵庫は完全記述のタイプの問題は出題されず、すべて記号穴埋めで許してくれるのでイージーです。
だからまずは、図形の証明問題に絞って対策することが最初のステップになります。使う問題集も基礎問系で全然OKで、証明のフローが頭に入っていて、記号であればスムーズに解けるレベルまで仕上げて欲しいです。
だから、ステップ式の中2と中3の図形分野をやり込みましょう。中2は合同、中3は相似なので、どっちもやってください。どちらが出るかはわかりません。ステップ式は穴埋め問題が比較的に多いので兵庫の大問対策にも向いています。
ここまでやってまだ余裕がある子は、図形特化の問題集「証明の達人」をやってもいいです。
結構難しいレベルの証明もあり完全記述なのですが、ここまでやり込めば兵庫の証明問題レベルはクソ雑魚に感じるはずです。
なお、兵庫県に限らず高校受験の数学の図形問題は根本的に難易度が高く、(1)の証明穴埋め以降の(2)〜(4)は極めて正解するのが難しくなります。正答率が1ケタ%の問題も多く、努力したって解けない問題もあります。
例年生徒を見ていますが、かなり優秀な生徒でも兵庫の図形問題を最後まで完答する子はまずいません。少なくとも最後の問題はほぼ100%に近い確率で落としてしまい、超優秀な子ですら満点は取らせられません。問題そのもののレベルが高すぎるのです。
なので、図形分野に限っては証明だけは絶対に正解できるようにしておき、あわよくば次の(2)までは解ければ儲け物ぐらいに思っておくのが健全です。
この図形分野にこだわっていくよりも、他分野の勉強時間を増やしたり、他教科の勉強時間を増やした方が受験トータルで得点できる期待値は確実に上がるはずです。
ほとんどの生徒にとって図形大問は、証明以外は捨て問になる可能性が高いということは覚えておくべきです。
思考力を問う大問:再現性のある対策は皆無
さあ、ラスト1つ。兵庫の場合、ここまで紹介した合計5つの大問に加え、一番最後に「思考力・応用力・判断力」を試す新傾向の問題が必ず出題されています。
こんな感じ↓です。


はい、これ見て色々思うところはあると思いますが、「文章が長い!!!!」ですよね。汗
正直、最後の大問はモロに子供の地頭チェックみたいになっています。会話形式の長い文章を読ませて、状況を読み込み、流れに従って問題に答えていくタイプです。共通テストを完全に意識しており、対策やパターンでは解けないように工夫されています。
当然こんなのは全受験生が初めて遭遇する問題であり、対策しておけば何とかなるとかそういう次元の話ではありません。一定の知能がない生徒は全く対応できず平気で大問全部落としてしまいます。
これはもう努力の問題ではなく才能格差の問題です。
だから、塾としてもこの最後の大問だけは再現性高く対策ができないから、ある程度は生徒を選ばないと高得点など取らせられるわけもなく、読解力や数的センスがない子はこの大問はドボンです。
ただ、(1)までならある程度文章が読める子なら正解できるので、ここは0点を回避して3〜6点ぐらいを取らせたいと思います。しかし再現性はないです。問題に依存しまくります。
それでも何とか対策したいという場合は、高校数学を少しかじるとかがある意味では再現性のある対策です。なぜなら、整数問題や数列が絡められることが非常に多いので、高校数学の考え方が分かっていると明らかに有利だからです。自分もたまにチートして等差数列の公式にはめたりして時短するので、そこまでやり込めれば強いです。
でも、そんな余裕があるのは上位層だけだし、そもそも上位層なら地頭で対策しなくてもそこそこ点数を取ってくるので、この話は誰が得するのかしていても分からなくなります。汗
いずれにせよ中間層以下は最後の大問は地獄ですので、そこ以外で何とか点数を積み上げることに意識を向けるべきです。こういう時に内申点が不足しているとかだともう無理ゲーなので、内申点だけは落とさないでください。
兵庫県公立高校入試:数学の対策の重要ポイント
ここまでは、各大問の傾向とそれに合わせた対策法&使用教材を紹介してきました。ここからは、以上を踏まえて、全体的にどう対策を組み合わせるのかの「まとめ」に入ります。
基本は小問集合と関数で手堅く稼ぐ
まず、受験数学は高得点を再現性高く取るのは上位層でも厳しい教科です。
努力すれば必ず解けるようになるという問題ばかりではなく、一定の地頭が必要な問題も多い上、初見で見るような問題も多く出題されてしまうからです。だから現実的な対策として、「対策しておけば取れる問題を全て取り切る」というのが全受験生に共通して求められることです。
具体的には以下の通り。
・小問集合(大問1)
・関数の定番問題
・図形の証明穴埋め
・確率の基礎問題
兵庫受験の場合、生徒の地頭にもよりますが、これらは対策によってある程度は再現性高く点数を積み上げていける領域です。だから、難問は全て捨てて、意識的に得点しやすい分野に絞って勉強時間を振り分けましょう。
捨て問があると割り切る
高校受験の数学は、他教科と異なり「捨て問」があります。
捨て問とは、正答率が極端に低く受験生の超上位の上澄しか得点するできない難問を指します。また、仮に正解できるとしても1問を解くのに時間がかかりすぎてしまい、パスしないとその他の問題に著しく支障が出る問題です。
何を捨て問にするかは受験生のレベルにもよりますが、ある程度共通して捨て問と呼べる問題もあります。
それは、小問集合(大問1)を除くその他の大問の最後の問題です。
まず大前提、図形分野の最後の問題はどの年でも難しく、いつ受けても捨て問になる子が受験生全体の95%ぐらいです。だからもう読まなくてもOKで、すぐに×つけて飛ばした方が賢いです。
しかし、図形分野に関わらずどの大問も最後の問題は極めて難易度が高く、結局のところほとんどの生徒は最後の問題を正解することなく終わります。たまにアタリの大問があって、年によっては最後まで完答できる時もありますが、それも運の問題です。
なので、普段の対策の中では各大問の最終問題は全部捨ててもいいです。その代わり、それ以外の(1)〜(3)までぐらいの正答率を上げる工夫と努力を死ぬほどしてください。
数学で現実的に得点できる期待値は知っておこう
兵庫に限らず、公立高校の数学は難問が確実に混ざっており、そもそも100点満点のテストになっていません。それどころか、数問は捨て問がある以上、体感的には80点ぐらいが満点では?とも思います。
一部の難関校(神戸高校レベル)を受ける子以外、公立2番手を受ける子ですら数学で80%を超すのは現実的にかなり厳しく、もちろん再現性高く取らせる方法も思いつきません。
だから、数学は高得点を稼げるような教科ではないと割り切るのが大事です。
一般的に、「神戸高校レベルの子で数学の上限は80点、御影レベルで数学が得意なら70点台、それ以下だと60点を取れれば万歳」というのが自分の正直な感覚です。
中堅校を受ける生徒(六アイなど)だと、数学に関しては平気で50点台に引きづりこまれ、数弱の生徒だと他教科は良くても数学だけは30点台や40点台になることも珍しくありません。
ただし、これは子供の努力不足ではなく、シンプルに問題の難易度が高く、一定の地頭がない子に取っては厳しい試験だというだけの話。悪く言えば才能不足で取れないのですが、それゆえ仕方ないのです。
そういう意味では、数学は足を引っ張らない程度に対策し、その他の教科と内申点で逃げ切る以外は再現性の高いアドバイスはできません。これで内申点もなく英語など高得点が取れる教科ですら点が低い子は残念ですが勝利条件を満たしません。
高校受験は、英語の出来不出来で志望校の下限が決まり、数学の出来不出来で上限が決まる競技だからです。
受験対策のゴールは過去問演習と全国高校入試問題正解
兵庫県の公立対策の数学では、最終ゴールは過去問です。
結局は最後は兵庫の過去問を回して実践レベルの問題になれるしかなく、ここまで紹介してきた問題集は全てそのアシストに過ぎません。
なお、過去問についてはエディックが出している以下の過去問を使うといいです。自塾でも採用しています。解説が一番分かりやすいので、数学の過去問としてはベストです。
また、数学を受験レベルまで引き上げる上で欠かせないのが、「全国高校入試問題正解」の数学シリーズです。他県で出題されている過去問を分野別に収録している優れもの。
基本的には御影高校以上の公立2番手ぐらいから使って欲しい問題集で、数学がある程度得意で70点以上を安定して取りたいと願う生徒(見込みがあると判断できる生徒)にのみおすすめしています。
ここまでやれば高校受験の数学の対策としてはやるだけやったと言えるでしょう。
総括:数学勉強法の全て&大問別問題集ルートまとめ
最後に、本記事のまとめを残しておきます。
■ 全体方針
- 数学は「満点を狙う教科ではなく、取れるところで確実に取る教科」
- 各大問に再現性の差があるため、大問別に対策を変える
- 捨て問の見極めと得点源の明確化が重要
- 基本方針は「小問集合」と「関数分野」で得点を稼ぐこと
■ 大問別対策
● 大問1:小問集合(全8問・24点)
- 難易度が低いため、数学が苦手でも満点を狙うべき
- 使用教材:
- 『大問1の完成』(好学出版)
- 『計算の達人』(計算シャッフル問題)
- 学習法:
- 夏休みに2/3を仕上げ、残りは通常授業で継続演習
● 関数分野(大問2つ)
- 1次関数(文章題)と2次関数(図形融合)
- 1次関数文章題は難化傾向あり→地頭が必要で再現性低い
- 2次関数はパターン問題が多く、再現性が高い
- 使用教材:
- 『関数の達人』(都麦出版)→中3夏から使用
- 『ステップ式 数学 中2・中3』(基礎固め用)
● 確率・データ分野(毎年1題)
- 出題比率は確率が圧倒的多数
- 問題傾向は「融合型」で難易度に年ごとの差あり
- 使用教材:
- 『ステップ式 数学 中2』
- 『WinPass 中2』(補強用)
- 『確率・データの達人』(応用用、12月目処に使用)
● 図形分野(毎年1題)
- (1)の証明問題が得点源、以降は難問になりがち
- 使用教材:
- 『ステップ式 数学 中2・中3』(合同・相似)
- 『証明の達人』(余裕ある生徒向け、記述問題あり)
● 思考力問題(毎年最後の大問)
- 長文・読解・判断を求められる新傾向型
- 対策困難で再現性なし(上位層しか対応不可)
- 0点回避のため**(1)だけは正解を狙う**
■ 対策のまとめと注意点
- 対策すべき得点源
- 小問集合(大問1)
- 2次関数
- 図形の証明
- 確率の基本問題
- 捨て問にすべき問題
- 各大問の(4)などの最終問題
- 思考力大問の(2)以降
- →無理に挑まず、他の問題に時間を振るべき
- 得点の目安(実感値)
- 神戸高校:80点が上限
- 御影高校:70点台で優秀
- 六アイなど中堅校:50〜60点でも十分
- 数弱層:30〜40点台でも珍しくない
■ 使用すべき最終演習教材
- 『兵庫県 公立高校入試 過去問』(エディック・創造学園)
- 『全国高校入試問題正解 分野別 数学』(旺文社)
※全保護者さんに読んで欲しい「勉強法や子育て本のおすすめ」を以下の記事で紹介中。Kindle Unlimitedを使うと全て”無料”で読むことができます。
※学習塾に通っていない場合は、塾用教材を使って勉強するのが効率的です。市販教材に比べて圧倒的に質が高くコスパもいいです。学習塾の先生の要望に応えた教材で、痒い所に手が届く良書ばかりです。本屋では買えないですが、Amazonなら購入可能なので、以下におすすめ教材をまとめておきます。
※市販教材でおすすめ教材を知りたい人には、以下におすすめ参考書・問題集をまとめた記事を掲載しておきます。
※高校受験おすすめコラムは以下の通りです。
・【高校受験】親ができること厳選3個紹介!後悔しない子供への接し方
・【高校受験】勉強するのが遅すぎた!手遅れになる子の特徴を解説
・中3からでも間に合う内申の上げ方や裏技が大嘘である理由と現実
・【高校受験】内申足りないから諦めるべきケース!逆転が厳しい場合
・内申点の平均はオール3ではなく〇〇!平均では全く安心出来ない理由
・中3の実力テストがやばい理由まとめ!点数が取れない子の特徴
・【高校受験】偏差値70トップ校に塾なしで受かる子の特徴&方法
・高校受験に向け小学生のうちにしておくこと一覧!塾長目線で解説
・【高校受験】最後に伸びる子の特徴!直前の追い上げで逆転する方法
・私立高校と公立高校の頭の良さ比較!同一偏差値ならどっちが頭いい?
・中3一学期の内申は厳しい?中3の1学期の成績が下がる理由&対処法











